1517. Simple Addition

Let’s define the next recursive function F(n), where

F(n) =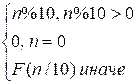

Let’s define the function S(p, q) as follows:

S(p, q) =

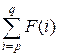
In this problem you have to calculate S(p, q) on given values of p and q.

Input. Consists of multiple test cases. Each line contains two nonnegative integers p and q (p ≤ q), separated by space. p and q will fit in 32 bit signed integer. Input is terminated by a line with two negative integers. This line should not be processed.

Output. For each input pair p and q print the value S(p, q) on a single line.

Sample input	Sample output
1 10 10 20 30 40 -1 -1	46 48 52

SOLUTION

recursion

Algorithm analysis

The function f(n) given in the problem statement finds the last non-zero digit of n. For example, f(1234) = 4, f(3900) = f(390) = f(39) = 9.

Let

g(p) =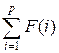

Then S(p, q) = g(q) – q(p – 1).

To compute the value of g(p), the sum of last significant digits for numbers from 1 to p, divide the numbers from 1 to p to three sets (‘/’ is an integer division):

1. Numbers from (p / 10) * 10 + 1 to p;

2. Numbers from 1 to (p / 10) * 10 that are not null-terminated;

3. Numbers from 1 to (p / 10) * 10 that are null-terminated;

The sum of the last significant digits in the first set equals to 1 + 2 + … + p mod 10 = t * (t + 1) / 2, where t = p mod 10. The sum of numbers in the second set equals to p / 10 * 45, because the sum of all digits from 1 to 9 equals to 45, and the number of full tens equals to p / 10. The required sum for the third set we shall find recursively: it equals to g(p / 10).We get a recurrence:

g(p) = + + 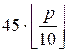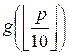, t = p mod 10

g(0) = 0

Example

If p = 32, the fist set contains the numbers 31, 32, the second contains 1, …, 9, 11, …, 19, 21, …, 29, and the third contains 10, 20, 30. The value t = 32 mod 10 equals to 2.

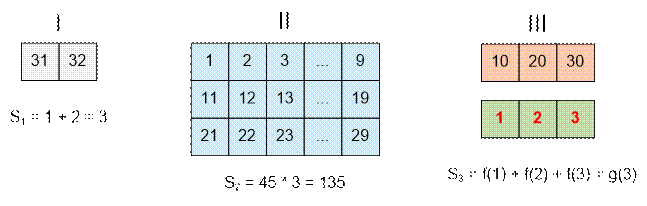
g(32) = + 45 * 5 + g(3) = 3 + 135 + (1 + 2 + 3) = 144

Let p = 1234.

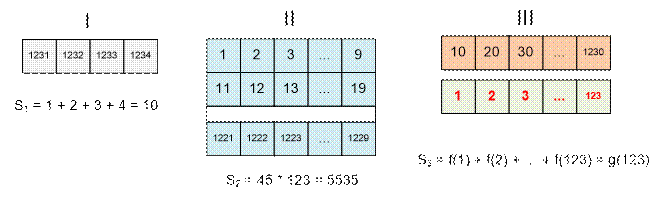
g(1234) = + 45 * 123 + g(123) = 10 + 5535 + g(123) = 5545 + g(123)

Computing the value g(123) = 595, we get:

g(1234) = 5545 + g(123) = 5545 + 595 = 6140

Algorithm realization

Since the processing is performed on 32-bit signed numbers, to avoid overflow in calculations we shall use long long type.

long long p, q;

The function g computes the sum of values of the function f(n) for argument n from 1 to p.

long long g(long long p)

{

long long t = p % 10;

if (p <= 0) return 0;

return t * (1 + t) / 2 + p / 10 * 45 + g(p / 10);

}

The value S(p, q) is determined as g(q) – q(p – 1).

long long s(long long p, long long q)

{

return g(q) - g(p - 1);

}

The main part of the program. For each pair of numbers p and q print the value s(p, q).

while(scanf("%lld %lld",&p,&q), p + q >= 0)

printf("%lld\n",s(p,q));

Java realization

import java.util.*;

public class Main

{

static long g(long p)

{

long t = p % 10;

if (p <= 0) return 0;

return t * (1 + t) / 2 + p / 10 * 45 + g(p / 10);

}

static long s(long p, long q)

{

return g(q) - g(p - 1);

}

public static void main(String []args)

{

Scanner con = new Scanner(System.in);

while(true)

{

long p = con.nextLong();

long q = con.nextLong();

if ((p < 0) && (q < 0)) break;

System.out.println(s(p,q));

}

con.close();

}

}

Python realization

The function g computes the sum of values of the function f(i) for argument i from 1 to n.

def g(n):

if n <= 0: return 0

t = n % 10

return (n // 10) * 45 + (t * (t + 1) // 2) + g(n // 10)

The main part of the program.

while True:

p, q = map(int, input().split())

if p < 0 and q < 0: break

For each pair of numbers p and q print the value s(p, q) = g(q) – g(p – 1).

print(g(q) - g(p - 1))